折り鶴パターンの等面四面体

昨日開催された第11回折り紙の科学・数学・教育研究集会で、東海大学の奈良先生がちょっとした面白い話をされていたので、その検証実験をしてみました。

「折紙探偵団」のWebページの背景には、折り鶴の形をした多角形がタイリングされています。

「折紙探偵団」のトップページ

背景に使われている折り鶴のタイリング（前川氏のデザイン）

タイリングされている鶴を1つ取り出すと、下図のような形をしています。
（縦横の比率がオリジナルと違います）

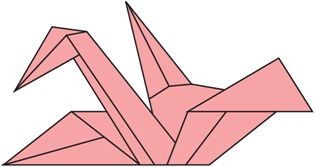
この形はタイリングできて、例えば、下図のように180度回転させたものとピッタリ接合できます。

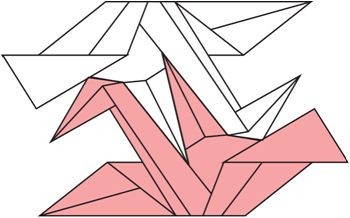
さらに、この状態で、左右の輪郭線の形がまったく同じであるため、左右を貼り合わせて円筒を作ることができます。

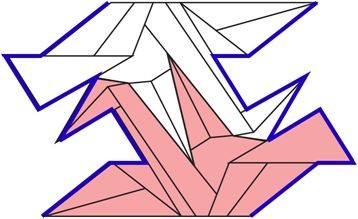
うまく説明できているかわかりませんが、円筒を作れる→それを開けば展開図は長方形になる→長方形から等面四面体（4つの面が全て合同な四面体）を作れる。という流れで、2つの折り鶴のパターンから等面四面体ができてしまいます。
というわけで、検証してみましょう。

折り鶴のパターンに四面体の展開図を重ねたところ。
（三角形が5つありますが、一番左と右の三角形が重なって1つの面になります）

試しに印刷して切り抜いたところ。

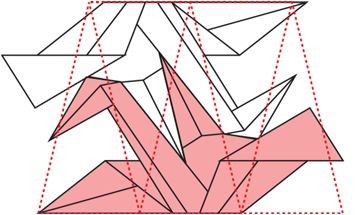
貼り合わせて四面体を作ってみました。隙間なく貼り合わせることができて、無事に等面四面体が完成。

追記：
奈良先生がおっしゃっていたのは、鶴のパターン「2つ」ではなく「1つだけ！」で四面体を作る話でした。私の勘違いでした。お恥ずかしい限り。この鶴のパターンをデザインした前川氏のブログで、1つの鶴のパターンから四面体を作る例と、もう少し詳しい話が紹介されています。1つだけでできた方が、はるかにスマートですね。
http://origami.asablo.jp/blog/2011/12/05/6234015