格子パターンの折りたたみ方の数え上げ(2)

今から2年半前に、次のようなパターンには、「平坦折り可能な折り線のパターン」がいくつ隠されているだろうか？
というようなことを考えたことがあります。
（当時のブログ）

平坦に折りたたみ可能なパターンの数は、（対称性や回転によって重なる事例を考慮せずに）単純に数え上げると166,254,336通りであるという結論を出したのですが、これが誤りであったことがわかりました。ああ。。

この誤りを指摘してくれたのは、研究室の山本君。
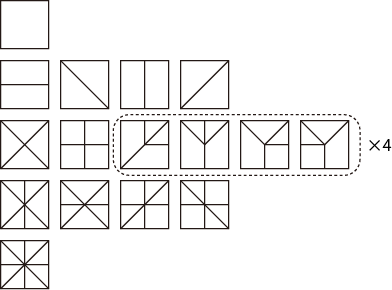
私が当時に挙げた平坦に折りたためる基本構造（下図）に不足があったということでした。

↓当時に挙げた平坦折り可能な基本パターン

不足していたのは下図に赤で追加した8つのパターン。

指摘されてみれば、まさにその通りで、どうしてこれを見落としていたのだろうか。。
山本君は、実際に折り紙を折って確認していたようで、やはり手を動かして確認しないとダメですね。

当時のプログラムコードをひっぱりだして、新しく追加した基本パターンを考慮して数え上げて、バグを見つけて修正して
さらに機能追加して対称性による重複を除外したところ、次のように結果が変わりました。
（局所平坦折り条件を満たしているパターンです）

4x4の構造の場合 259,650,300通り (2014年12月時点の計算)

というわけで、冒頭の折り線パターンには、局所平坦折り条件を満たしているユニークなパターンが約2億6千万通りあることがわかりました。

これから、大局的に折れるパターンを拾い上げて、折った後の形を調べると・・・どれくらいの数になるのでしょうか？
引き続き山本君に頑張ってもらいましょう！